Practicando la inversión

La Inversión en Dibujo Técnico es una transformación geométrica en la que a una figura corresponde otra y en la que se cumple que:

El producto de la distancia de un punto al Centro de Inversión por la distancia de su  inverso al Centro de Inversión es constante (K) y se llama Potencia de Inversión. Esto quiere decir que OA·OA’ = OB·OB’ = OT·OT = K

Para afrontar la resolución de ejercicios de inversión, lo primero que debemos observar es si la inversión está definida y como, esto nos podrá dar ideas de como abordar la solución. Consideramos que la inversión está definida cuando conocemos:

• El centro y un par de puntos homólogos (A, A’) 
• El centro y la potencia de inversión (k). La circunferencia con centro el centro de inversión y radio raíz de K, la llamaremos circunferencia de autoinversión.

Las principales características de este tipo de inversión son que:

• Dos puntos inversos (A, A’) están alineados con un punto fijo llamado Centro de Inversión (O)
• Si k>0, los puntos homólogos están situados al mismo lado del centro de inversión. Si k<0, los puntos homólogos están situados a a distinto lado.
• Las perpendiculares a la circunferencia de autoinversión son circunferencias dobles, pero no circunferencias de puntos dobles.

En este tipo de transformación sucede que:

• La inversión de una recta que pasa por el centro de inversión es otra recta que coincide con la primera. Diremos que es una recta doble, aunque no lo son sus puntos.
• El inverso de una recta que no pasa por el centro de inversión es una circunferencia que si pasa por el centro de inversión, y cuyo centro está en la perpendicular que pasa por el centro de inversión.
• El inverso de una circunferencia que pasa por el centro de inversión es una recta que no pasa por el centro de inversión y que es perpendicular a la recta que une sus centros.
• El inverso de una circunferencia que no pasa por el centro de inversión, es otra circunferencia que tampoco pasa por el centro de inversión.

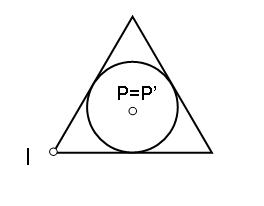
Os propongo la siguiente tanda de ejercicios sobre un triángulo y su circunferencia inscrita, en los que iremos colocando en diferentes posiciones el centro de inversión (I) y un punto y su inverso que coinciden (P=P')

CASO 1

El centro (I) y el punto P y su homólogo (P=P') se sitúan sobre los vértices de un triángulo.

CASO 2

El centro (I) se sitúa en un vértice y el punto P y su homólogo (P=P') sobre un punto de tangencia con la circunferencia inscrita.

CASO 3

El centro (I) se sitúa en un vértice y el punto P y su homólogo (P=P') sobre un punto de tangencia con la circunferencia inscrita, de manera que comparten el mismo lado del triángulo.

CASO 4

El centro (I) se sitúa en un vértice y el punto P y su homólogo (P=P') en el centro incentro.

CASO 5

El centro (I) se sitúa en el incentro y el punto P y su homólogo (P=P') en  uno de los vértices del triángulo.

CASO 6

El centro (I) se sitúa en el incentro y el punto P y su homólogo (P=P') en uno de los puntos de tangencia con la circunferencia inscrita.

A continuación puedes ver un fichero PDF con la propuesta de ejercicios anterior.